2.6. Номинальные и реальные показатели. Индексы цен

2.6.1. Номинальные величины и проблемы сопоставимости показателей

Для анализа динамики макроэкономических показателей необходимо, чтобы их значения в различные периоды были сопоставимы. Сопоставление стоимостных показателей не представляло бы проблем в условиях постоянных цен. Однако цены динамичны, причем цены на различные товары и услуги меняются неодинаково (см. рис. 2.20). Показатели, рассчитываемые в ценах, демонстрирующих такую неустойчивость, вряд ли можно сравнивать.

Например, при сравнении валового выпуска Украины (в основных ценах) за 2006 год (1182179 млн.грн.) с соответствующим показателем 2007 года (1565055 млн.грн.), необходимо установить, имел ли место рост объемов выпуска, и сколько процентов прироста он составил. Однако показатели 2006 и 2007 года будут отличаться не только потому, что изменились объемы производства, но и потому, что цены на произведенные товары и услуги в 2007 году будут отличаться от цен 2006 года.

Макроэкономические показатели, рассчитанные в текущих рыночных ценах, являются номинальными величинами, поскольку их реальное значение искажается ценовым фактором. Для примера рассмотрим гипотетическую экономику, в которой производится единственный товар – станки. В 2006 году рыночная стоимость одного станка составляла 20 тыс. грн., а в 2007 году цена выросла до 30 тыс. грн. При этом в 2006 году экономика произвела 100 станков, а в 2007 году – 80.

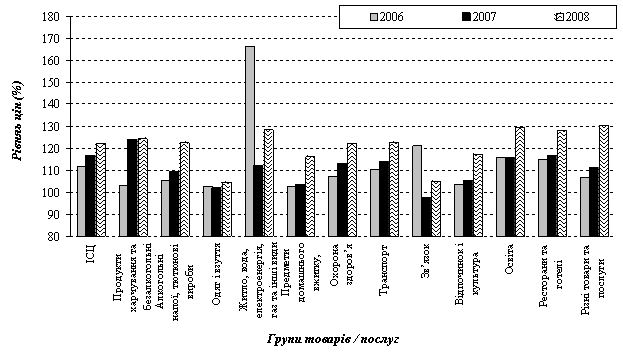
Рис. 2.20. Уровень цен по группам товаров / услуг в Украине за 2006–2008 годы (в декабре расчетного года по сравнению с декабрем предыдущего года)

 

Номинальный ВВП в 2006 году будет 2 млн. грн., а в 2007 году – 2,4 млн. грн. Номинальное значение показателя выросло, в то время как на самом деле в 2007 году экономика произвела меньшее количество станков. Рост номинального значения ВВП обусловлен ростом цен.

В этом примере легко привести два значения ВВП к сопоставимому виду: достаточно определить, насколько выросла цена станка в 2007 году по сравнению с ценой 2006 года (индекс цен):

 

.

 

Теперь легко определить реальное значение ВВП 2007 года, пересчитав его в сопоставимых ценах:

 

,

 

откуда получаем, что реальное значение ВВП 2007 года будет равно 1,6 млн.грн., т.е. меньше, чем ВВП 2006 года (2 млн.грн.).

При оценке уровня доходов возникает аналогичная проблема: зачастую рост номинальной заработной платы работника сопровождается ухудшением его материального положения, поскольку цены на потребительские товары и услуги растут значительно быстрее, чем зарплата.

Таким образом, возникает необходимость оценки влияния ценовых факторов на показатели: 1) объемов национального производства; 2) доходов населения.

Для статистического изучения динамики цен используется индексный метод, с помощью которого рассчитываются агрегатные*  индексы цен – показатели, характеризующие, насколько вырос общий уровень цен в экономике; в первом случае – на промышленные (инвестиционные) товары и услуги, во втором – на потребительские товары и услуги.

Индекс промышленных цен называется дефлятором ВВП. Индекс цен на потребительские товары и услуги называется индексом потребительских цен.

2.6.2. Понятия весовой структуры, базисного и расчетного периодов

Индекс потребительских цен рассчитывается методом потребительской корзины. Потребительская корзина – это набор товаров и услуг массового потребительского спроса, который устанавливается Госкомстатом Украины на основании данных о денежных расходах всех домохозяйств (как городских, так и сельских).

Весовая структура потребительской корзины (весовые коэффициенты) – доля потребительских расходов на покупку товаров (услуг) в общем объеме потребительской корзины, которая определяется на основе фактических потребительских расходов домохозяйств в денежном выражении;.

Например, предположим, что условная корзина состоит из 4-х продуктов, и ее стоимость составляет 100 грн. Денежные расходы домохозяйств на первый продукт составляют 10 грн., на второй – 25 грн., на третий – 30 грн. и на четвертый – 35 грн., то, соответственно, весовые коэффициенты для этих товаров в корзине будут 10, 25, 30 и 35 %.

Критериями включения товаров (услуг) в потребительскую корзину являются:

– наличие значительного спроса на эти товары (услуги);

– регулярное наличие их в свободной продаже.

Территориальные органы статистики осуществляют сбор информации о товарах и ценах и расчеты средних цен по региону для каждого из товаров (услуг), включенных в потребительскую корзину, а так же территориальных индексов цен.

Базисный период весовой структуры – период времени, к которому относится рассчитанная весовая структура. Действительно, структура потребительских расходов домохозяйств не остается неизменной даже в условиях постоянного дохода и постоянного уровня цен. Меняются потребительские предпочтения, появляются новые товары и т.д. В условиях роста цен структура потребления меняется тем более: если рост дохода отстает от роста уровня цен, то потребление каких-то товаров (услуг) будет сокращаться, что приведет к возрастанию удельного веса других, жизненно необходимых товаров (услуг).

Базисный период индекса – период времени, для которого значение индекса принимается равным 1,0 (или 100%). Это означает, что цены товаров (услуг) других периодов будут рассматриваться относительно цен базисного периода (выше или ниже). Базисным периодом индекса может быть год, квартал, месяц. Например, на графиках рис. 2.20 базисным периодом для расчета индекса цен в декабре 2006 года является декабрь 2005 года, для декабря 2007 года – декабрь 2006 года, и т.д. Это позволяет установить, насколько выше или ниже был уровень цен на соответствующие группы товаров (услуг) год назад. Если же в качестве базисного периода берется предыдущий месяц, то индекс показывает, как изменился уровень цен в течение одного месяца. Поскольку цены меняются неравномерно в течение года, то можно установить, в какие месяцы наблюдался наибольший рост цен.

Потребительская цена (тариф) – фактическая цена (тариф) на товар (услугу), реализуемые в свободной продаже с учетом НДС, акциза и прочих косвенных налогов. Для конечного потребителя цена, по которой он приобретает товар (услугу), может значительно отличаться от основной цены, которую получает производитель (продавец), за счет косвенных налогов, поступающих государству.

2.6.3. Индекс потребительских цен

Поскольку количества различных потребительских товаров (колбасы, холодильников и подсолнечного масла) не сопоставимы в натуральном исчислении (килограммах, штуках и литрах), для построения агрегатного индекса цен рассматривается их удельный вес в совокупном объеме проданных товаров в стоимостном выражении. Агрегатный индекс цен отражает неоднородность совокупности.

Для иллюстрации методики расчета индекса потребительских цен приведем пример. Предположим, что семья составила полный перечень своих покупок за месяц. Всего получилось 300 товаров (услуг)* . Общая стоимость на момент составления набора (базисный период весовой структуры) составила  грн. Количество каждого товара (услуги), включенного в набор, будем обозначать , где . Цены товаров (услуг), включенных в набор, будем обозначать , где . Тогда стоимость набора на момент его составления (базисный период):

 

.

Весовые коэффициенты  товаров (услуг) в наборе:

 

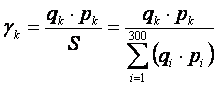.                                                           (2.13)

 

Если через год эта семья посчитает стоимость составленного набора по новым ценам (расчетного периода), обнаружится расхождение со стоимостью корзины в базисном периоде:

 

.

 

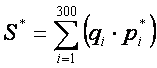Отношение стоимости набора в расчетном периоде к его стоимости в базовом периоде и будет индексом цен (ф. 2.14):

 

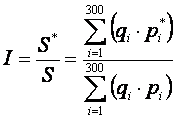                                                                    (2.14)

 

Индекс цен с весами базисного периода получил название*  индекса Ласпейреса, по имени немецкого статистика Э. Ласпейреса (1834–1913), который предложил формулу для его расчета.

 

                                                                (2.15)

 

В формуле (2.15) указаны количества товаров (услуг) базисного периода. В статистических расчетах используются весовые коэффициенты базисного периода, определяемые по формуле (2.13).

 

                                                                (2.16)

 

Очевидно, что индекс Ласпейреса не учитывает изменение структуры потребления в расчетном периоде по сравнению с базисным. В результате он в значительно большей степени будет отражать рост цен на товары и услуги, имевшие наибольший удельный вес в потребительской корзине в базисном периоде, в то время, как их удельный вес в корзине расчетного периода может значительно сократиться, а удельный вес других товаров и услуг – возрасти.

Для примера рассмотрим гипотетический случай, когда набор потребительских товаров включает всего 2 позиции. В базисном году количество первого товара () было 10 ед., а количество второго товара () было 100 ед. В базисном году первый товар стоил 100 грн. ( = 100 грн.), а в расчетном году его цена () выросла до 105 грн. за единицу. Второй товар стоил в базисном году 1 грн. за единицу ( = 1 грн.), а в расчетном году его цена () выросла до 5 грн. Для упрощения предположим, что количества первого и второго товаров, потребляемых в расчетном периоде, остались теми же, т.е.  = 10 ед.,  = 100 ед.

Вычислим весовые коэффициенты товаров для базисного и расчетного года. Для  базисного года весовая структура набора:

 

;

.

Весовая структура набора в расчетном году:

;

.

 

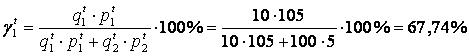Сравнивая весовую структуру наборов базисного и расчетного периодов (при этом количества товаров в расчетном году остались такими же, как и в базисном), замечаем, что удельный вес второго товара очень значительно вырос.

Теперь рассчитаем индекс цен по формуле (2.15):

 

.

А ели рассчитать этот индекс, используя весовые коэффициенты () базисного периода по формуле (2.16), то получим совершенно иное значение:

 

.

 

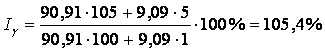Если теперь предположить, что второй товар является товаром первой необходимости, то мы обнаружим, что для сохранения потребления второго товара на прежнем уровне необходимо сократить потребление первого товара на 4 единицы (в предположении неизменного дохода). В этом случае общая сумма расходов изменится незначительно (с 1100 грн. в базисном году до 1130 грн. в расчетном периоде). Это означает, что покупательная способность дохода потребителя снизилась на 4 единицы первого товара. Таким образом, индекс, рассчитанный на основании весовых коэффициентов базисного периода (105,4 %) в данном гипотетическом примере дает нам заниженную оценку сокращения покупательной способности дохода по сравнению с оценкой (140,91 %) по формуле (2.15).

Если цены на оба товара изменились пропорционально, то расчетные значения, полученные по формуле (2.15) и по формуле (2.16) будут совпадать.

Если же цена на первый товар в расчетном периоде выросла более значительно, чем на второй товар, то индекс, рассчитанный по формуле (2.15), будет незначительно отличаться (в большую сторону) от индекса, рассчитанного с использованием весовых коэффициентов по формуле (2.16).

 

Задание для самостоятельной работы:

 

1) Рассчитайте оба варианта индекса – по формулам (2.15) и (2.16) – по данным предыдущего примера при условии, что цена на первый товар в расчетном периоде () выросла до 140 грн. за ед., а цена второго товара () не изменилась.

2) Рассчитайте оба варианта индекса для предыдущего примера – по формулам (2.15) и (2.16) – при условии, что цена на первый товар в расчетном периоде () выросла до 180 грн. за ед., а цена второго товара () снизилась до 0,8 грн. за единицу.

2.6.4. Реальное значение показателя дохода

Теперь осталось определить формулу для расчета реального дохода с учетом вычисленного значения индекса потребительских цен:

 

                                                                                (2.17)

 

где  – реальный располагаемый доход домохозяйств,  – номинальное значение располагаемого дохода,  – индекс потребительских цен (по типу индекса Ласпейреса).

Реальный доход отражает покупательную способность номинального дохода. Рассмотрим пример.

Предположим, что в 2006 году номинальный доход домохозяйства составлял 1000 грн., а в 2007 году значение номинального дохода выросло до 1200 грн. При этом индекс потребительских цен в 2007 году по отношению к базисному периоду 2006 года составил 150 %. Тогда реальный доход домохозяйства в 2007 году будет:

 

 

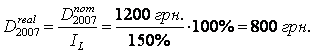
Очевидно, что хотя номинальный доход домохозяйства вырос, реальный доход сократился (с 1000 грн. до 800 грн.).

Индекс потребительских цен (consumer price index – ) является важнейшим индикатором, используемым не только для оценки уровня инфляции, но и для проведения социальной политики государства, в частности – защиты доходов населения от инфляции путем их индексации.

На базе значений индексов потребительских цен рассчитывается темп изменения стоимости жизни () по формуле:

 

                                                               (2.18)

 

где  – индекс потребительских цен расчетного периода;  – индекс потребительских цен базисного периода. В табл. 2.15 приведены значения индекса потребительских цен и рассчитанные на основе этих данных по формуле (2.18) темпы изменения стоимости жизни.

Таблица 2.15

Індекси споживчих цін у 1999 – 2007 рр.

(до відповідного періоду попереднього року, %)

* дані Держкомстату України

 

 

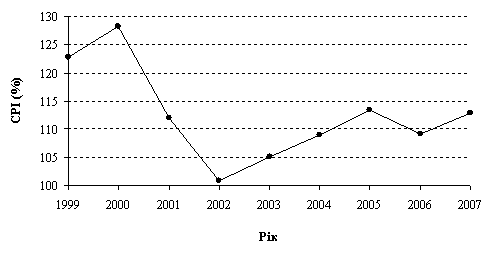
Рис. 2.21. Динамика индекса потребительских цен () в Украине

 

 

 

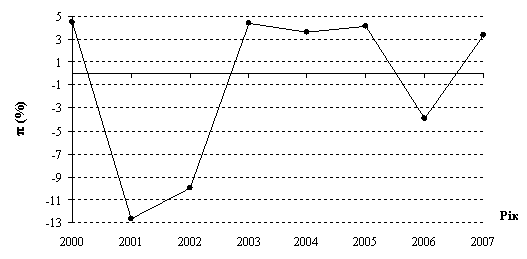
Рис. 2.22. Динамика темпов роста стоимости жизни в Украине с 2000 по 2007 год

 

Отрицательные значения темпов роста стоимости жизни свидетельствуют о том, что рост цен на потребительские товары и услуги в рассматриваемом периоде замедлился по сравнению предыдущим периодом.

Для более глубокого изучения инфляционных процессов Госкомстат Украины использует альтернативный ценовой индикатор – базовый индекс потребительских цен. Этот индекс позволяет минимизировать эффекты шоков предложения, сезонных колебаний цен на отдельные продукты (услуги) и государственного регулирования цен. Базовый индекс потребительских цен рассчитывается методом исключения из набора, используемого при расчете индекса потребительских цен, ряда товаров и услуг на основе экспертных оценок специалистов Госкомстата Украины, Национального банка Украины и Министерства экономики Украины.

Базовый индекс потребительских цен (БИПЦ) является производным индексом от индекса потребительских цен и характеризует уровень инфляции, который формируется под воздействием монетарных условий. Главной целью расчета этого индекса является определение стойкой динамики цен с минимизацией влияния краткосрочных неравномерных изменений цен, вызванных шоками предложения или административной регуляцией. Таким образом, БИПЦ в наибольшей степени характеризует инфляцию, которая вызвана давлением со стороны спроса, и, соответственно, наиболее полно отображает эффекты от изменения реальных монетарных условий.

В табл. 2.16 приведены данные Госкомстата Украины о значениях индексов цен: базового индекса потребительских цен и  в 2009 г.

Таблица 2.16.

БІСЦ та ІСЦ у 2009 році

(відсотків)

 

Наблюдая динамику обоих индексов (рис. 2.23, 2.24), можно заметить, что, как правило, значения базового индекса потребительских цен немного выше, чем ИПЦ (за исключением июня и октября 2009 года, рис. 2.24).

 

 

Рис. 2.23. ИПЦ и БИПЦ (в % к декабрю предыдущего года)

 

 

Рис. 2.24. ИПЦ и БИПЦ (в % к предыдущему месяцу)

 

Реальные монетарные условия – агрегированный эффект реальных процентных ставок и реального эффективного обменного курса, т.е. основные направления влияния монетарной политики.

2.6.5. Дефлятор ВВП

До сих пор мы рассматривали расчет индекса цен, исходя из корзины базисного периода. Однако при расчете индекса цен можно использовать набор товаров (услуг) не базисного, а расчетного периода *  :

 

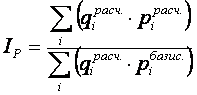                                                                 (2.19)

 

Такой индекс называется индексом Пааше по имени немецкого статистика Г. Пааше (1851–1925).

С использованием весовых коэффициентов формула расчета этого индекса выглядит следующим образом:

 

,                                                                (2.20)

 

где весовые коэффициенты   рассчитываются по формуле (2.13) для корзины базисного периода.

Формула определения индекса цен с весовыми коэффициентами расчетного периода применяется при вычислении дефлятора ВВП, или индекса промышленных цен. С помощью этого индекса значение  номинального ВВП (в текущих рыночных ценах) выражается в сопоставимых ценах, т.е. дефлируется:

 

,                                                                                 (2.21)

 

в результате чего полученное значение реального ВВП () можно сравнивать (сопоставлять) со значением ВВП базисного периода (рис. 2.25).

 

 

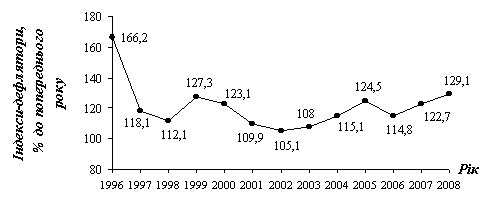
Рис. 2.26. Динамика значений дефлятора ВВП в Украине

 

Индексы промышленных цен рассчитываются не только для экономики в целом, но и по отраслям национального хозяйства. Это позволяет отслеживать изменение ценовых пропорций между отраслями. В частности, можно отследить диспаритет цен между производством сельскохозяйственной продукции и промышленными отраслями (см. табл. 2.17 и 2.18).

Таблиця 2.17

Індекси цін виробників промислової продукції у 2003 – 2008 рр.

(до попереднього року, %)^*

* Держкомстат України

Таблиця 2.18

Індекси цін реалізації сільськогосподарської продукції у 2009 році

(сільськогосподарські підприємства (крім малих); % до відповідного періоду 2008р.)*

* Держкомстат України

 

На рис. 2.26 показаны кривые, отражающие динамику индексов цен производителей различных отраслей народного хозяйства Украины в 2009 г.

 

 

Рис. 2.26. Динамика значений индексов цен сельскохозяйственной продукции и продукции других отраслей народного хозяйства в 2009 году

2.6.6. Сравнение агрегатных индексов цен. «Идеальный» индекс

Отличие индекса–дефлятора ВВП от индекса потребительских цен () заключается не только в том, что для расчета  используются весовые коэффициенты базисного периода, а для расчета дефлятора ВВП – весовые коэффициенты расчетного периода. Состав «корзины» промышленных товаров значительно отличается от потребительской корзины не только количественно, но и качественно. В «промышленную» корзину включаются все товары и услуги, произведенные в национальной экономике в расчетном году (ВВП). Потребительская корзина, в отличие от «промышленной», включает импортные товары (услуги).

В табл. 2.19 приведены значения индекса потребительских цен и индекса промышленных цен по месяцам 2009 года. Рис. 2.27–2.30 иллюстрируют расхождения между значениями индексов цен в 2008 – 2009 годах в зависимости от базисного периода (расчет индексов рис. 2.27–2.28 производился относительно предыдущего месяца, а рис. 2.29–2.30 – относительно декабря предыдущего года).

Табл. 2.19

Індекси споживчих цін та цін виробників промислової продукції у 2009 році

 

Рис. 2.27. Индексы потребительских цен и цен производителей промышленной продукции по месяцам 2008 г. (к предыдущему месяцу) – по данным Госкомстата Украины

 

 

Рис. 2.28. Индексы потребительских цен и цен производителей промышленной продукции в 2009 г. (к предыдущему месяцу)

 

 

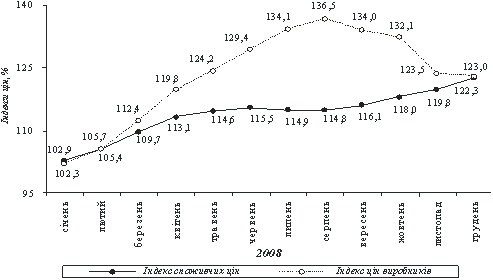
Рис. 2.29. Индексы потребительских цен и цен производителей промышленной продукции в 2008 г. (к декабрю предыдущего года)*  

 

 

Рис. 2.30. Индексы потребительских цен и цен производителей промышленной продукции в 2009 г. (к декабрю предыдущего года)* 

 

Для сравнения двух типов индекса (Ласпейреса и Пааше) рассмотрим тот же пример, что и при расчете индекса Ласпейреса. Для начала отследим, как меняются значения индексов в зависимости от изменения корзины расчетного периода при одном и том же изменении цен (первый товар подорожал на 5%, а второй – в пять раз).

В данном примере результаты расчетов индексов Ласпейреса и Пааше с весовыми коэффициентами по формулам (2.16) и (2.20) значительно отличаются от значений, рассчитанных по формулам (2.15) и 2(19), при этом значение индекса Ласпейреса (105,4 %) меньше значения индекса Пааше (106,9 %).

При вычислении индексов Ласпейреса и Пааше по формулам (2.15) и (2.19) их значения будут совпадать, если количества товаров в корзине расчетного периода не меняется или меняется пропорционально, например, сокращается на 10% (табл. 2.20).

Таблица 2.20

Пример расчета индексов Ласпейреса и Пааше

* По формулам (2.15) и (2.19)

** По формулам (2.16) и (2.20)

 

Однако если количество первого товара сократится более значительно, чем второго (например, в расчетном году количество первого товара сократится на 20%, а второго – на 10%), то при тех же изменениях цен, которые были рассмотрены ранее, значение индекса Пааше будет больше, чем значение индекса Ласпейреса (табл. 2.21).

Таблица 2.21

Расчет индексов Ласпейреса и Пааше

* По формулам (2.15) и (2.19)

** По формулам (2.16) и (2.20)

 

Если же количество второго товара изменится более значительно, чем количество первого (например, количество первого товара сократится на 10%, а второго – на 20%), то значение индекса Ласпейреса будет больше значения индекса Пааше (табл. 2.22).

Значения индексов, рассчитанные с весовыми коэффициентами по формулам (2.16) и (2.20), не только значительно меньше, чем индексы, вычисленные по формулам (2.15) и (2.19), но и демонстрируют устойчивое соотношение – во всех рассмотренных вариантах значение индекса Пааше, рассчитанное по формуле (2.20), больше значения индекса Ласпейреса, рассчитанного по формуле (2.16).

Таблица 2.22

Расчет индексов Ласпейреса и Пааше

* По формулам (2.15) и (2.19)

** По формулам (2.16) и (2.20)

 

Значительный разрыв между значениями индексов, вычисленных по формулам (2.15) и (2.17), с индексами, рассчитанными по формулам (2.16) и (2.20), обусловлен тем, что цена второго товара выросла в расчетном периоде в пять (!) раз. Для случая более умеренного роста цен различия в значениях этих индексов не так существенны (табл. 2.23). При многократном росте цен на отдельные товары (услуги) агрегатные индексы, рассчитанные с весовыми коэффициентами по формулам (2.16) и (2.20), будут значительно занижать реальный рост уровня цен (см. табл. 2.22).

Таблица 2.23

Расчет индексов Ласпейреса и Пааше

* По формулам (2.15) и (2.19)

** По формулам (2.16) и (2.20)

 

Дальнейшие расчеты, которые предлагается сделать самостоятельно, показывают, что при пропорциональном изменении цен на все товары (например, если цены на все товары возрастут на 20%), значения индексов, рассчитанные по формулам (2.15), (2.16), (2.19) и (2.20) будут совпадать.

На основании проведенного исследования поведения индексов Ласпейреса и Паше можно сделать вывод, что оба индекса обладают определенными недостатками: индекс Ласпейреса не учитывает структурные изменения в потреблении в расчетном периоде, а индекс Пааше в большей степени отражает изменение цен на товары и услуги расчетного периода.

Индекс потребительских цен учитывает цены импортных товаров, в то время, как дефлятор ВВП – только те товары (услуги), которые были произведены в национальной экономике.

Рассмотрим подробнее факторы, влияющие на масштаб расхождений между значениями индексов Ласпейреса и Пааше. Покажем, что между динамикой цен и весовыми коэффициентами базового и расчетного периодов существует взаимосвязь. Для этого используем формулу весовых коэффициентов (2.13). Рассмотрим разность между весовым коэффициентом –го товара (услуги) в базисном () и расчетном периоде ():

.

Поскольку суммы в знаменателе (расходы) зависят, в основном, от дохода в базисном () и расчетном () периоде, то это выражение можно переписать так:

 

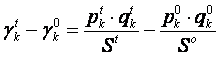
При этом, если цена –го товара (услуги) растет:

 

, где > 0,

 

то, как правило, его количество снижается (не увеличивается):

 

, где > 0.

 

Тогда:

 

.

 

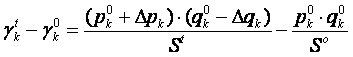Введем обозначение: . Тогда:

 

.

 

Разделим числитель и знаменатель дроби на  и вынесем произведение  множителем перед дробью (для этого разделим на это выражение числитель). Тогда получим:

 

, или

 

  

Введем обозначения:

  – для удельного прироста дохода,

  – для удельного прироста цены,

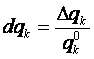  – для удельного прироста количества товара.

После подстановки этих обозначений получим:

                                (*)

Учитывая, что :

.

Вынесем  в числителе за скобки:

Однако выражение:

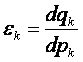
является коэффициентом ценовой эластичности спроса, откуда, соответственно, . Дальнейшие преобразования с учетом этого коэффициента позволяют получить такое выражение:

 

,

 

или, перенося  из левой в правую часть равенства:

 

                                                 (2.22)

 

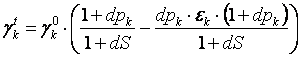
Очевидно, что данная формула может быть использована для случаев, когда , поскольку весовые коэффициенты не могут принимать отрицательных значений. Таким образом, при значительных ценовых колебаниях и высокой эластичности спроса товар–представитель просто исключается из «корзины» (весовой коэффициент  = 0).

Вообще говоря, эластичность спроса не является постоянной величиной: в зависимости от насыщения рынка данным товаром (услугой) чувствительность спроса к понижению цены товара снижается, т.е. снижение цены дает все меньший прирост объема совокупного спроса. При наличии значительного дефицита товара на рынке спрос также становится неэластичен, т.е. увеличение цены не приводит к ощутимому сокращению спроса. Поэтому, как правило, кривая эластичности спроса имеет вид (рис. 2.31):

 

 

Рис. 2.31. Эластичность спроса в зависимости от насыщения рынка

 

При  (неэластичном спросе) это выражение приближается к следующему:

,

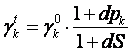что означает, что в случае неэластичного спроса весовой коэффициент товара–представителя растет с ростом цены. Предположим, что цена выросла на 10%, а доход увеличился на 20%:

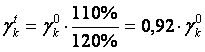
Если же цена выросла на 20%, а доход – на 10%, то:

При  это выражение приобретает вид:

 

.

 

Из формулы (2.22) очевидно, что весовые коэффициенты зависят от ценовой эластичности спроса  на товар (услугу), процентного изменения цены  и прироста дохода  (или общей суммы расходов). Получается, что изменение весовых коэффициентов расчетного периода относительно базисных весовых коэффициентов определяется ценовыми факторами и фактором дохода.

Отсюда можно сделать вывод, что при расчете агрегатных индексов цен по формулам Ласпейреса и Пааше возникает проблема: весовые коэффициенты в формулах (2.16) и (2.20) являются функциями цен, и их изменение в расчетном периоде (по сравнению с базисным) будет зависеть от ценовой эластичности спроса и прироста общей суммы расходов.

Для случая, когда общая сумма расходов в расчетном периоде сохраняется на том же уровне, что и в базисном (), формула (2.22) упрощается:

 

, или:

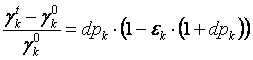
                                                             (2.23)

или:

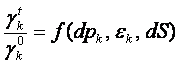                                                                    (2.24)

Моделируя функцию (2.24) в программе Microsoft Excel, установим влияние переменных ,  и  на изменение весового коэффициента в расчетном периоде относительно весового коэффициента базисного периода (рис. 2.32 и 2.33).

 

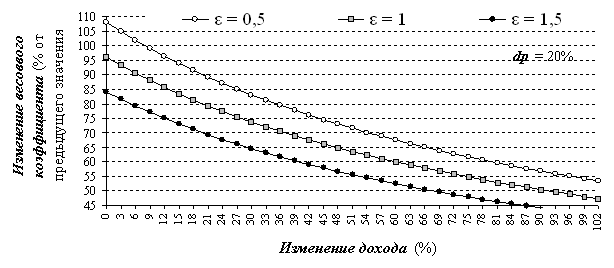
Рис. 2.32. Изменение значений весового коэффициента товара (услуги) в зависимости от изменения дохода при постоянном значении прироста цены (10 %) и трех различных значениях коэффициента эластичности спроса

 

Если зафиксировать изменение цены товара–представителя (например, 20 %), то можно установить, как влияет возрастание дохода на изменение весового коэффициента в расчетном периоде относительно базисного. На рис. 2.32 показана такая зависимость при различных значениях коэффициента ценовой эластичности спроса.

Как видно из графиков рис. 2.32, при отсутствии роста дохода в расчетном периоде (точка 0 по оси абсцисс) для случая низкой эластичности спроса ( = 0,5) весовой коэффициент расчетного периода даже больше базисного (108 %); при  = 1 весовой коэффициент расчетного периода составляет 96 % от значения весового коэффициента базисного периода; при  = 1,5 весовой коэффициент расчетного периода составляет всего 84 % от значения весового коэффициента базисного периода. С ростом дохода отношение весовых коэффициентов расчетного и базисного периодов (2.24) снижается.

Фиксируя прирост дохода (например, на уровне 10%), установим, как меняется выражение (2.24) при росте цены. На рис. 2.33 можно увидеть, что чем выше коэффициент ценовой эластичности, тем значительнее будет влияние изменения цены на снижение значения весового коэффициента (2.24).

При снижении цены эта зависимость выглядит совершенно иначе. Из рис. 2.34 видно, что при  ≤ 1 чем больше снижается цена, тем больше снижается значение весового коэффициента в расчетном периоде, а при  > 1 чем больше снижается цена, тем выше значение весового коэффициента расчетного периода.

Учитывая тот факт, что ценовая эластичность спроса на различные товары может отличаться существенно, можно сделать вывод о том, что установленная зависимость весовых коэффициентов от цены, дохода и ценовой эластичности делает формулы расчета агрегатных индексов цен весьма несовершенными с точки зрения отражения снижения или роста реальной покупательной способности дохода.

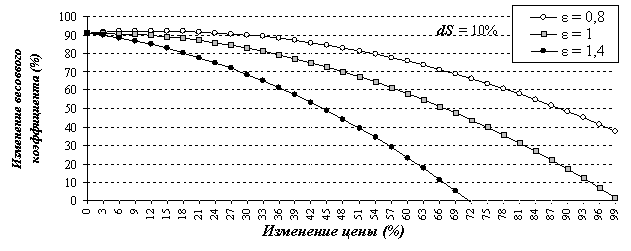
Рис. 2.33. Изменение значений весового коэффициента товара (услуги) – представителя в зависимости от изменения цены при одном и том же значении прироста дохода (10 %)

 

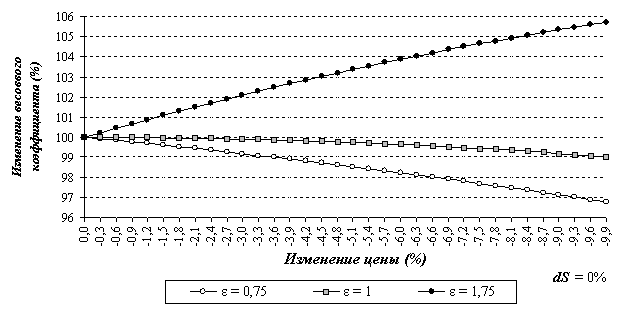
Рис. 2.34. Изменение значений весового коэффициента в зависимости от равнозначного изменения цены при отсутствии прироста дохода (0 %)

 

Поскольку с ростом цены значения весовых коэффициентов расчетного периода снижаются, то произведение цены на весовой коэффициент в расчетном периоде будет ниже, чем в базисном. Подставляя выражение (2.22) в формулу Пааше (2.20), можно установить функциональную зависимость расхождение между индексом Пааше и Ласпейреса от динамики цен и ценовой эластичности спроса. В значительной степени это различие определяется вариацией количественных изменений: если структура потребления меняется существенно, расхождения между значениями индексов становятся более ощутимыми. В незначительной степени расхождение между значениями индексов Ласпейреса и Пааше  вызваны вариациями цен.

Товары с высокой ценовой эластичностью будут значительно влиять на значение индекса Ласпейреса в случае роста цены.

Рис. 2.35. Изменение удельного веса товара–представителя в корзине при изменении цены

 

Очевидно, что наилучший линейный индекс лежит между индексами, вычисленными по формулам Ласпейреса и Пааше. Попытки зарубежных статистиков найти «идеальную» формулу для расчета агрегатного индекса цен привели к появлению формулы Эджуорта–Маршалла, в которой весовые коэффициенты являются средним арифметическим весов корзины базового и расчетного года:

 

                                                               (2.22)

 

Однако формула Эджуорта–Маршалла связана с несколько условной структурой потребительской корзины, не характерной ни для одного реального периода.

Наиболее удачным вариантом «золотой середины» между индексами Ласпейреса и Пааше считается «идеальный» индекс Фишера:

 

,                                                                            (2.23)

 

который оценивает не только набор товаров базисного периода по ценам текущего, но и набор товаров текущего периода по ценам базисного. Этот индекс используется при значительном изменении весовой структуры  в расчетном периоде по сравнению с весовой структурой базисного периода.

 

Задание для самостоятельной работы

Исследуйте поведение индексов Ласпейреса и Паше при снижении цен. Для этого заполните нужные ячейки таблицы 2.20. Сделайте выводы.

Таблица 2.20

Задание для расчета значений весовых коэффициентов и индексов Ласпейреса и Паше

* По формулам (2.15) и (2.19)

** По формулам (2.16) и (2.20)

 

Таблица 2.21

Решение задания на расчет значений весовых коэффициентов и индексов Ласпейреса и Паше

* По формулам (2.15) и (2.19)

** По формулам (2.16) и (2.20)